
Analysis
An assortment of topics loosely related to the field of analysis
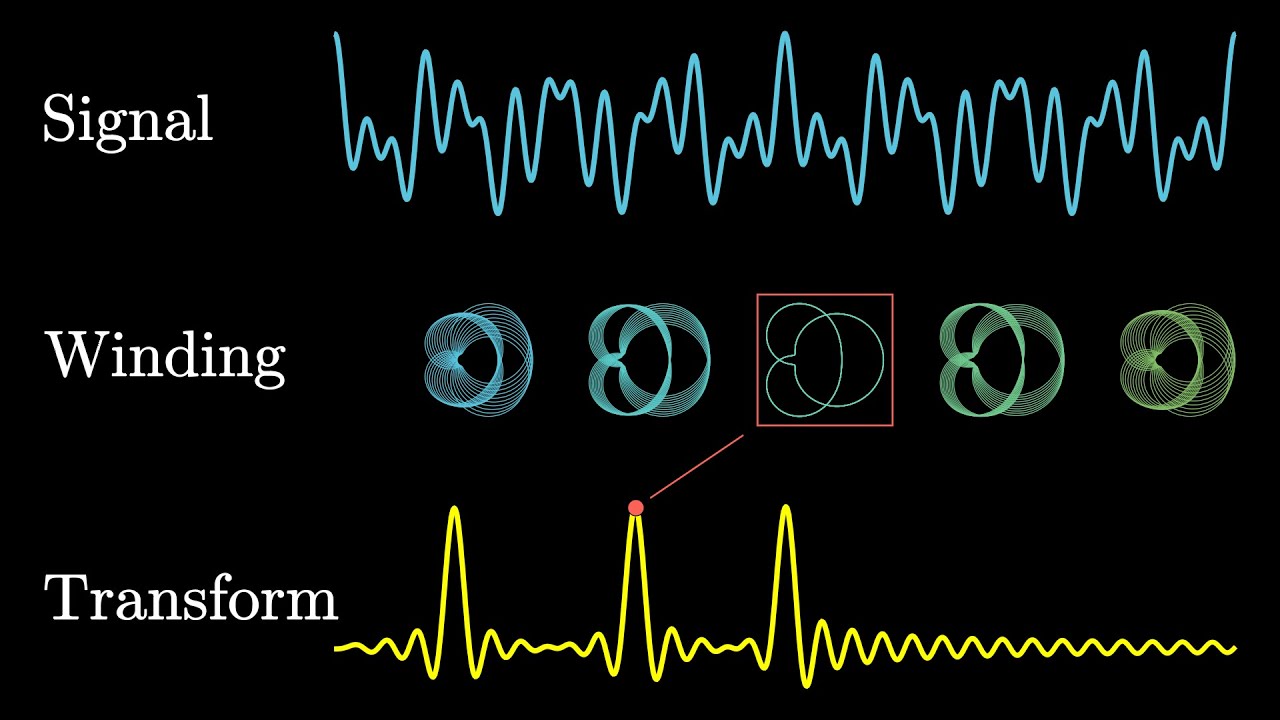
But what is the Fourier Transform? A visual introduction.An animated introduction to the Fourier Transform, winding graphs around circles.Jan 26, 2018

The more general uncertainty principle, beyond quantumThe general uncertainty principle, about the concentration of a wave vs the concentration of its fourier transform, applied to two non-quantum examples before showing what it means for the Heisenberg uncertainty principle.Feb 25, 2018

Newton's Fractal (which Newton knew nothing about)A surprising fractal that arises from Newton's method for finding roots of polynomials.Oct 12, 2021
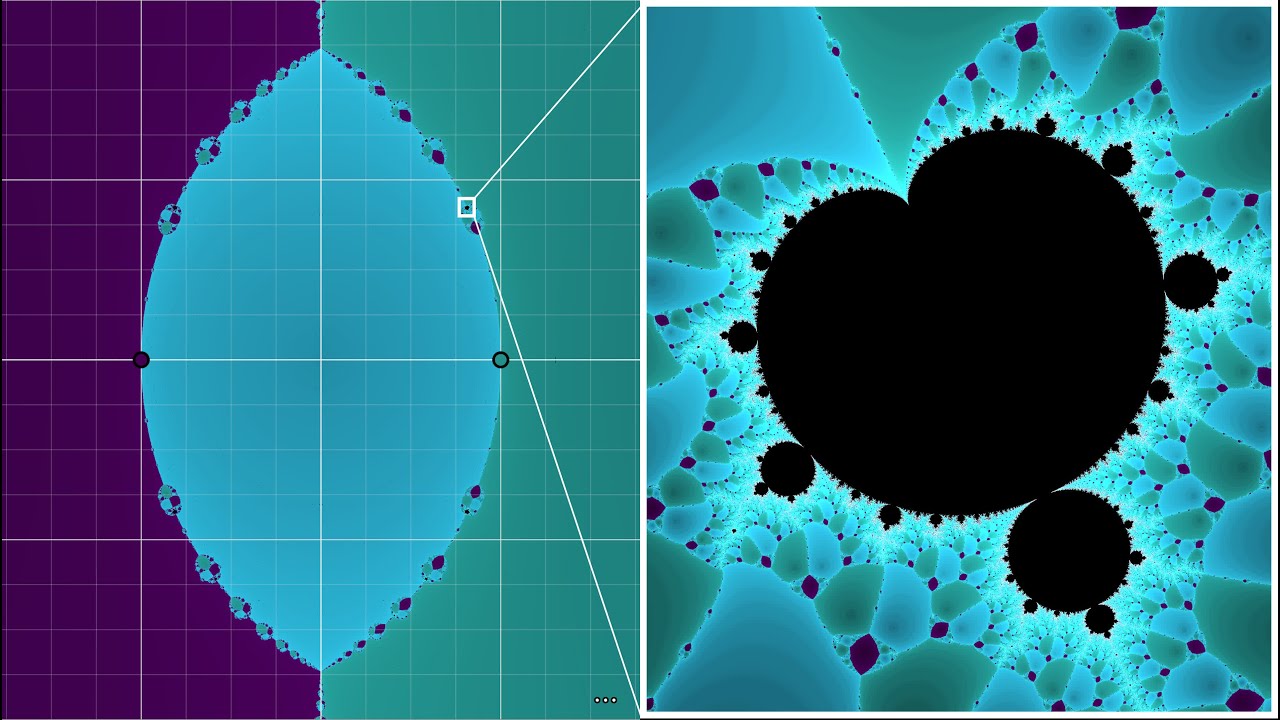
How a Mandelbrot set arises from Newton’s workAn introduction to holomorphic dynamics, which studies iterative processes in the complex plane.Oct 16, 2021
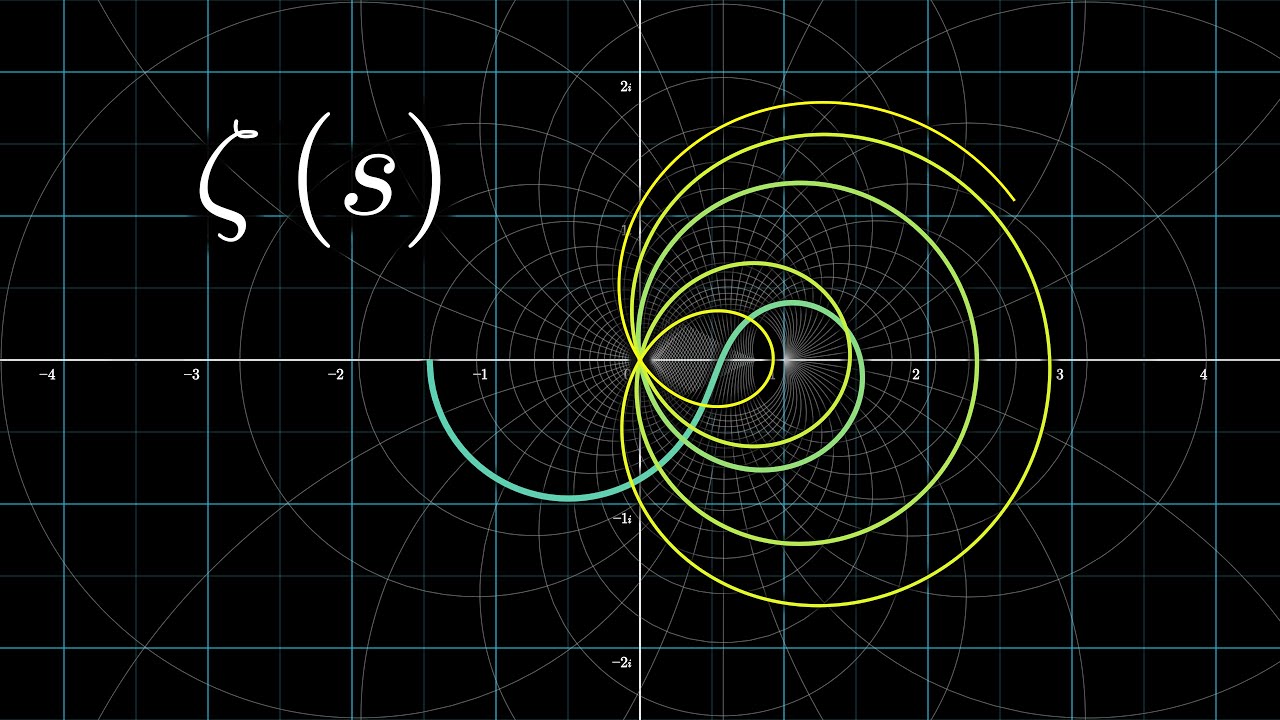
Visualizing the Riemann zeta function and analytic continuationWhat is the Riemann zeta function? What is analytic continuation? This video lays out the complex analysis needed to answer these questions.Dec 9, 2016

Divergence and curl: The language of Maxwell's equations, fluid flow, and moreDivergence, curl, and their relation to fluid flow and electromagnetismJun 21, 2018
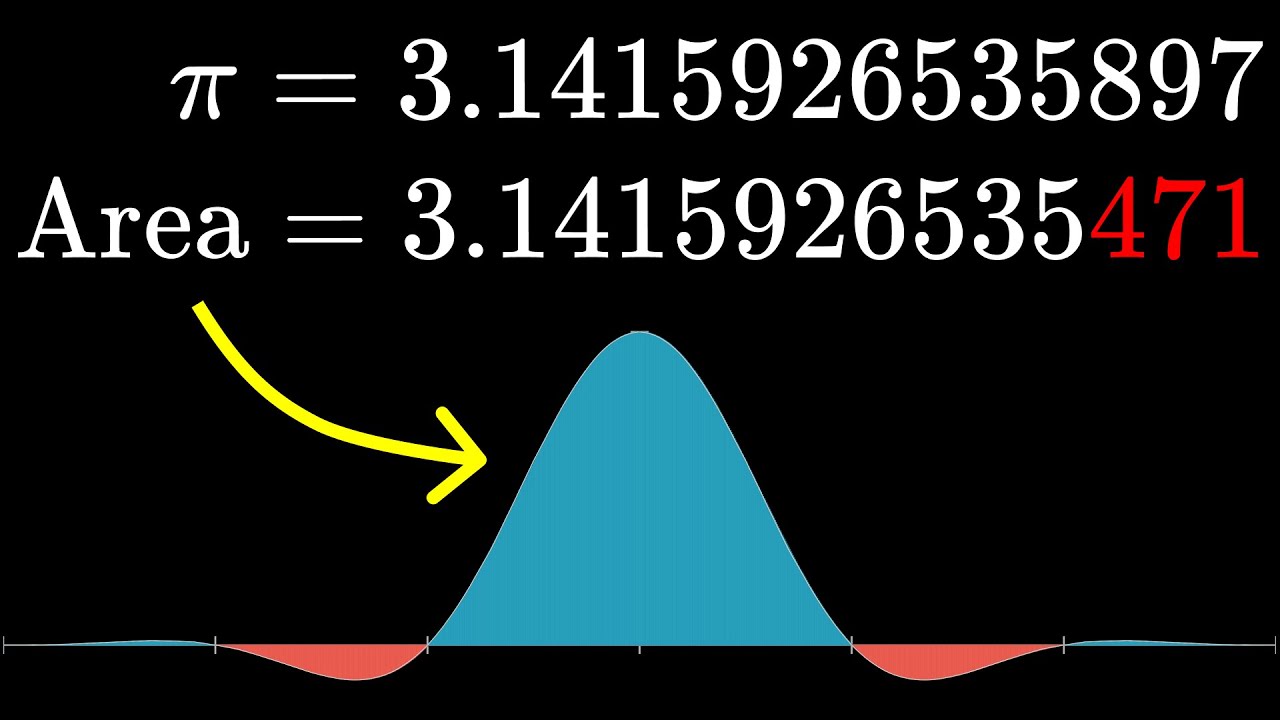
Researchers thought this was a bug (Borwein integrals)A curious pattern of integrals that all equal pi...until they don't.Nov 4, 2022
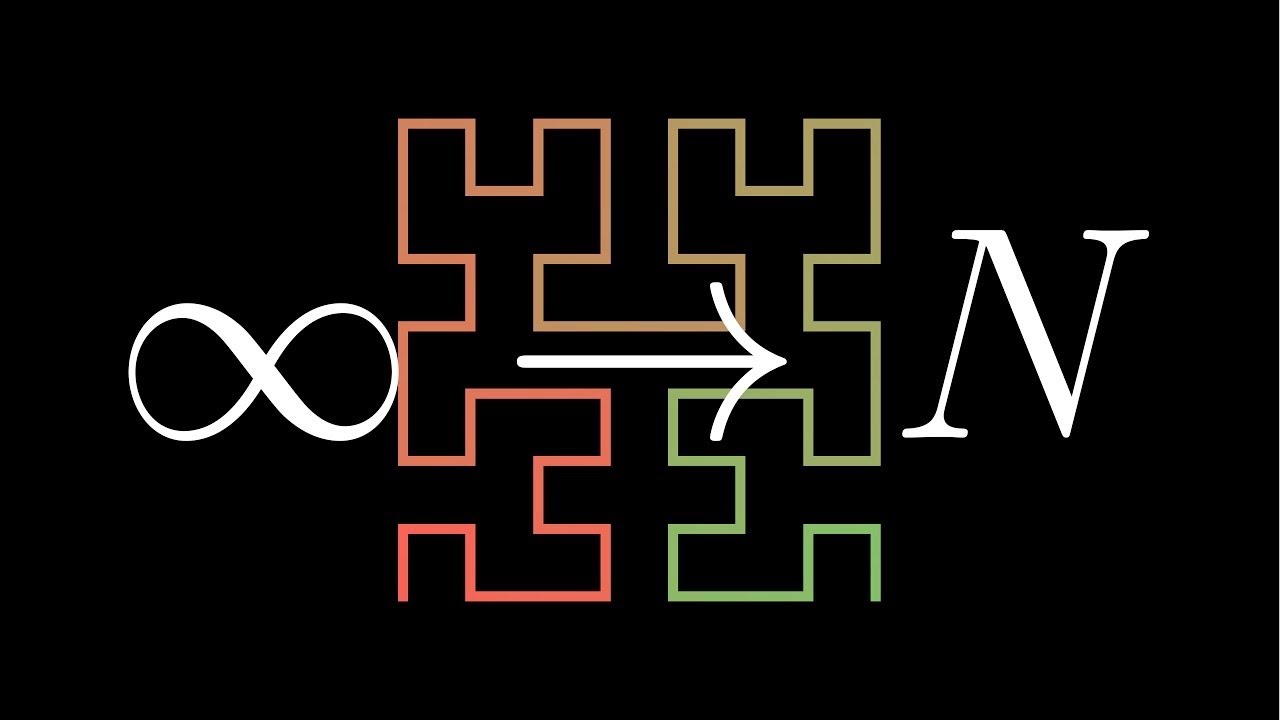
Hilbert's Curve: Is infinite math useful?Drawing curves that fill all of space, and a philosophical take on why mathematics about infinite objects can still be useful in finite contexts.Jul 21, 2017

Fractals are typically not self-similarWhat exactly are fractals? A common misconception is that they are shapes which look exactly like themselves when you zoom in. In fact, the definition has something to do with the idea of "fractal dimension".Jan 27, 2017
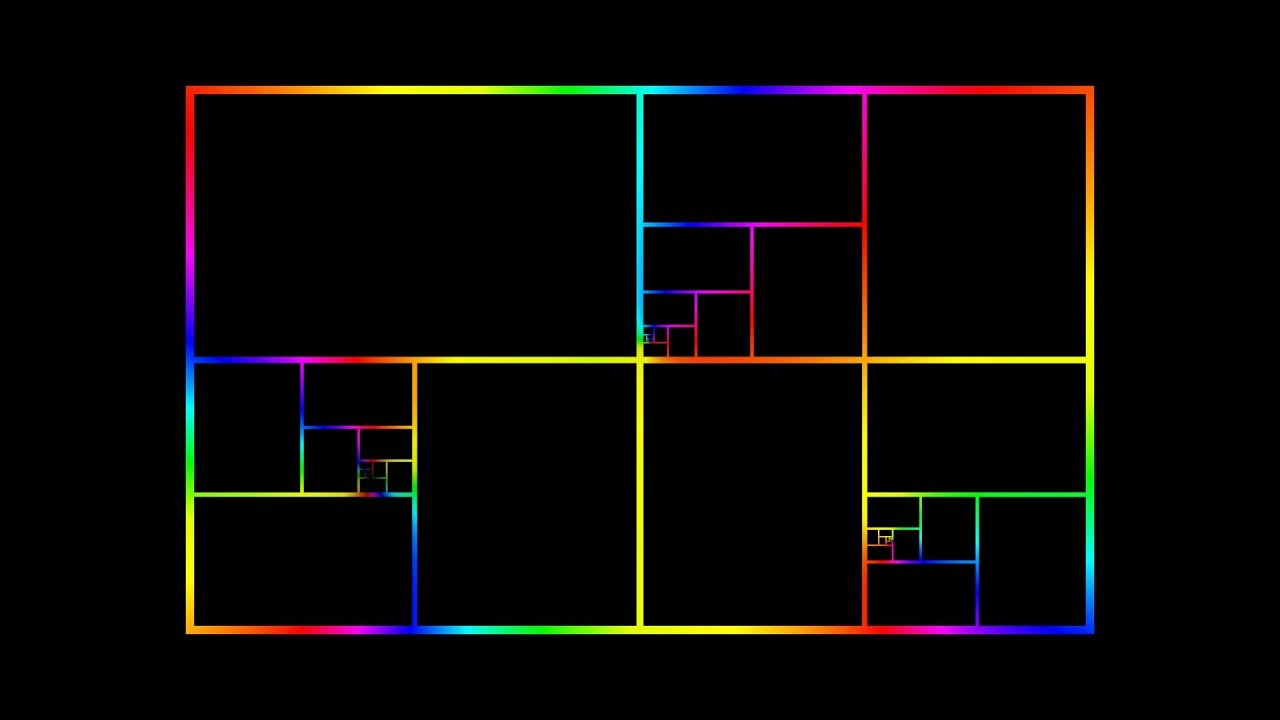
Winding numbers and domain coloringAn algorithm for solving continuous 2d equations using winding numbers.Mar 24, 2018
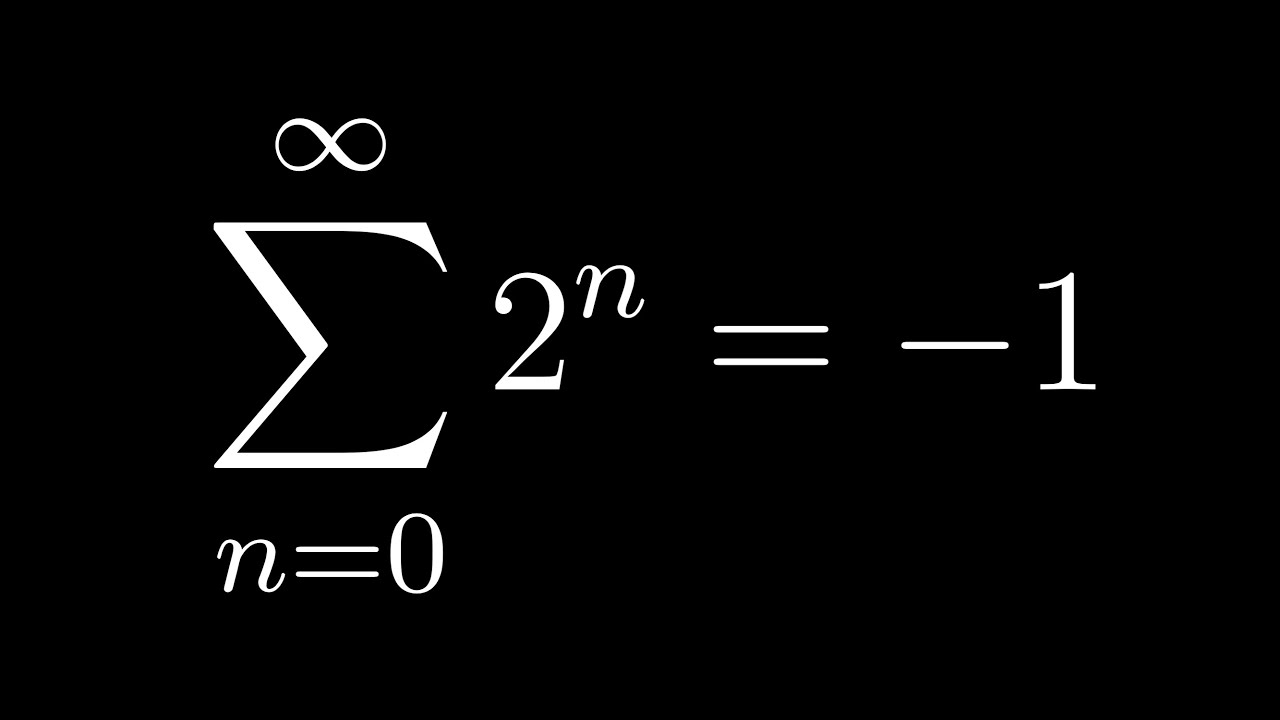
What does it feel like to invent math?A journey through infinite sums, p-adic numbers, and what it feels like to invent new math.Aug 14, 2015
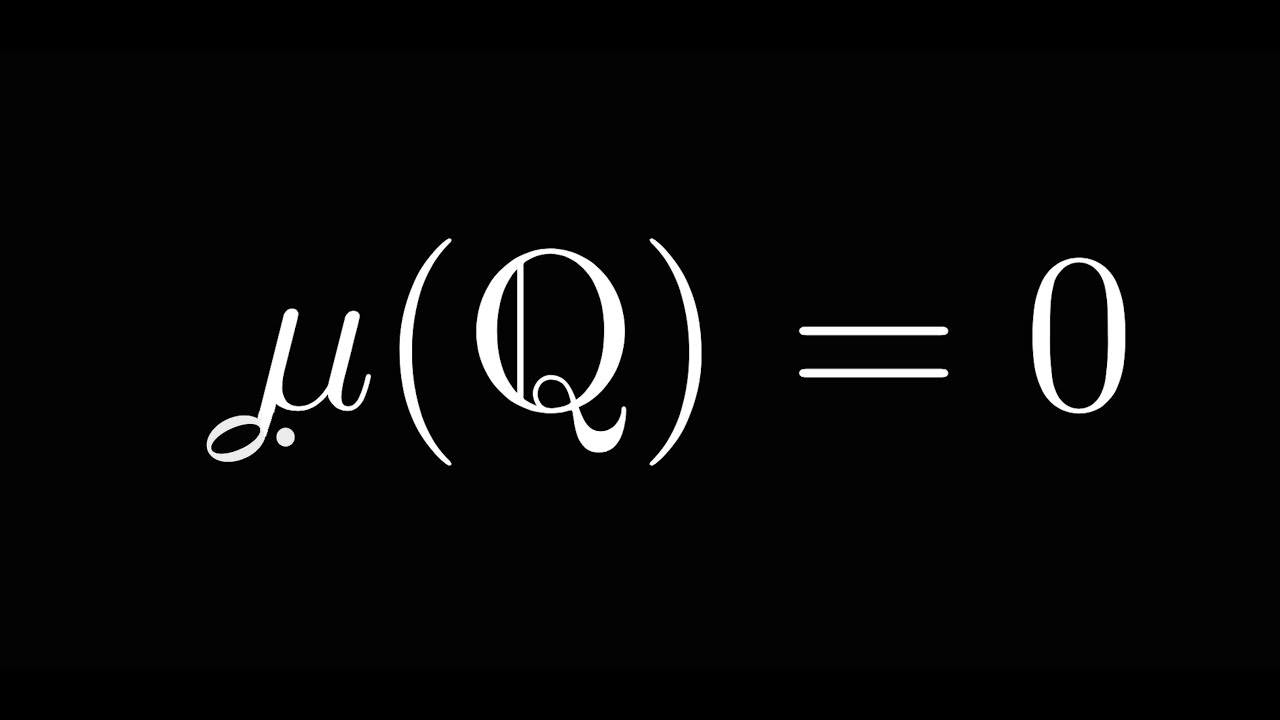
Music And Measure TheoryHow one of the introductory ideas in a field called "measure theory" can be thought of in terms of musical harnomy and dissonance.Oct 4, 2015