Why Pi
Why does pi show up in so many unexpected places?
The most unexpected answer to a counting puzzleA puzzle involving colliding blocks where the number pi, vey unexpectedly, shows up.
Why colliding blocks compute piTwo colliding blocks compute pi, here we dig into the physics to explain why.
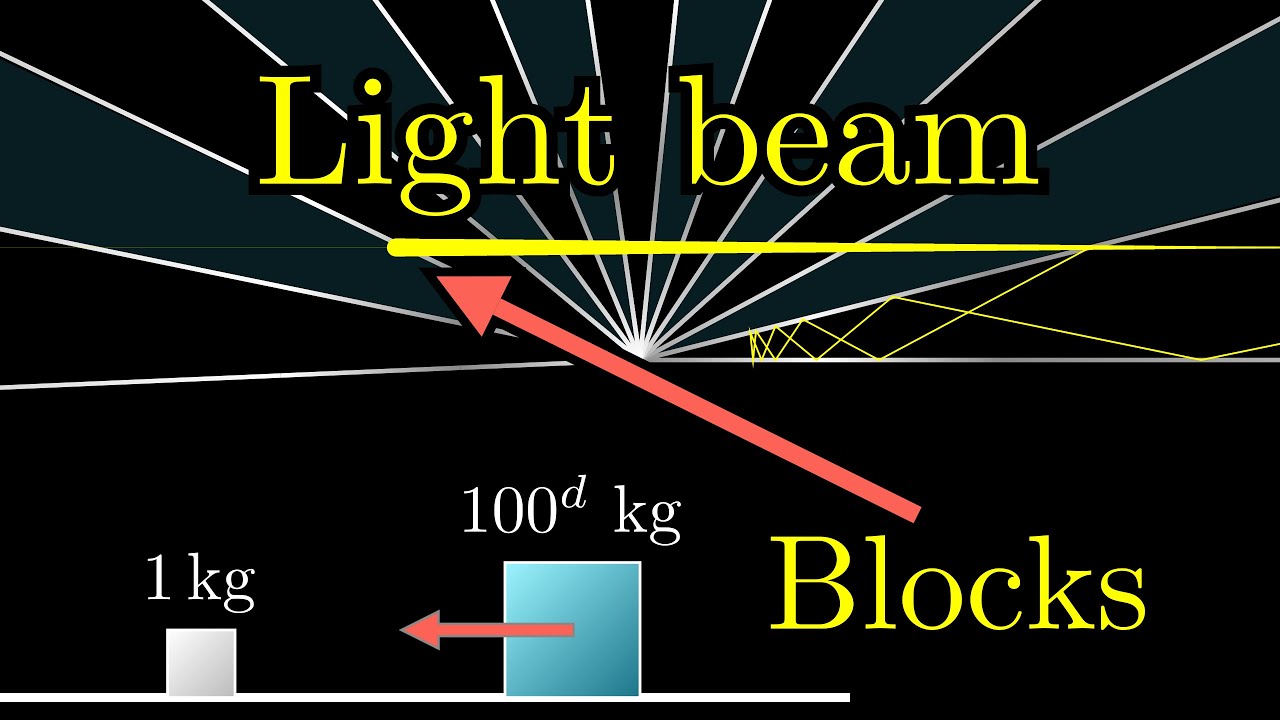
How colliding blocks act like a beam of light...to compute pi.The third and final part of the block collision sequence.
Why is pi here? And why is it squared? A geometric answer to the Basel problemA beautiful solution to the Basel Problem (1+1/4+1/9+1/16+...) using Euclidian geometry. Unlike many more common proofs, this one makes it very clear why pi is involved in the answer.
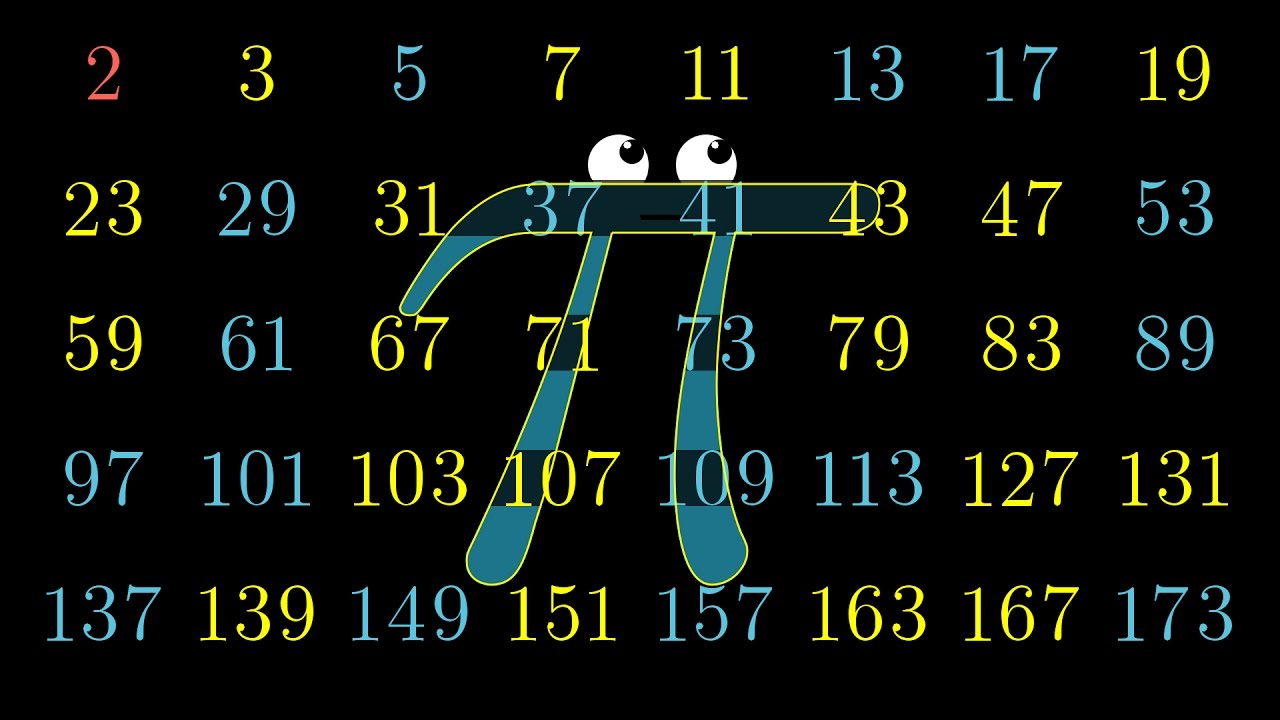
Pi hiding in prime regularitiesA beautiful derivation of a formula for pi. At first, 1-1/3+1/5-1/7+1/9-.... seems unrelated to circles, but in fact, there is a circle hiding here, as well as some interesting facts about prime numbers in the context of complex numbers.
Why π is in the normal distribution (beyond integral tricks)A classic proof explaining the pi in a Gaussian distribution, combined with a derivation of that distribution, the Herschel-Maxwell derivation, that explains why the proof is reasonable.
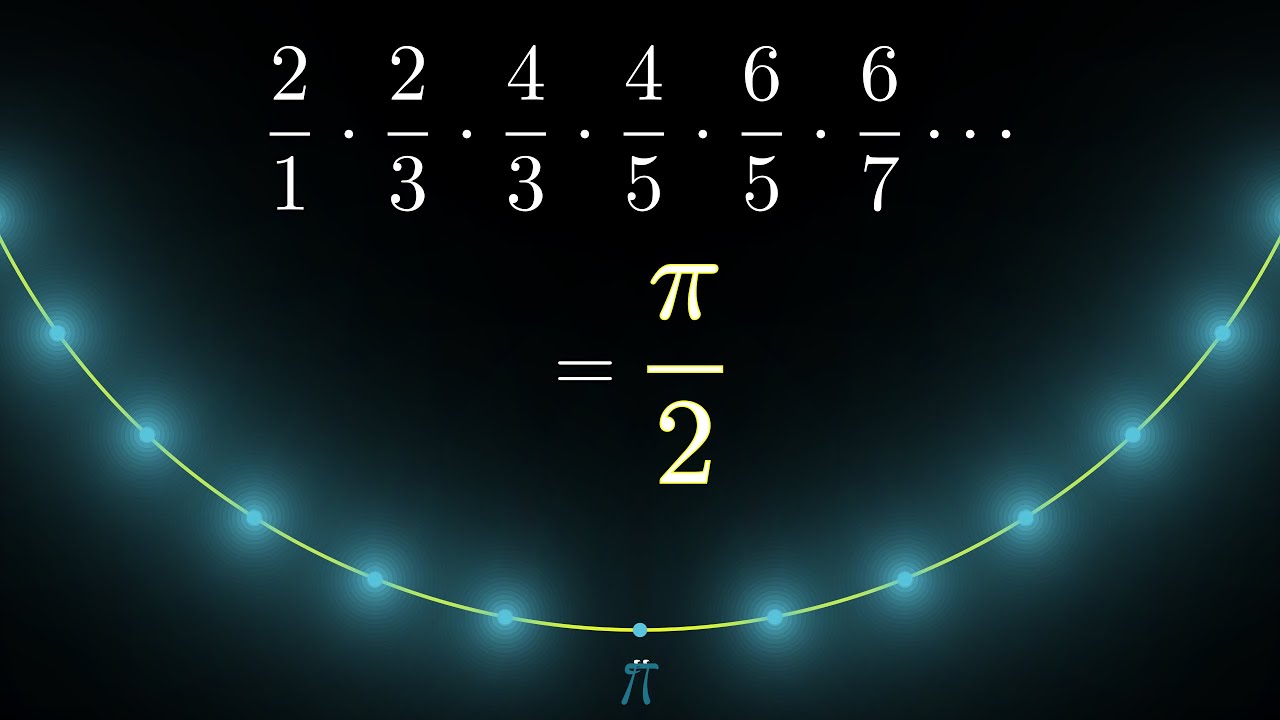
The Wallis product for pi, proved geometricallyA proof of the Wallis product for pi, together with some neat tricks using complex numbers to analyze circle geometry.
How pi was almost 6.283185...A bit of the history behind how we came to use the symbol "pi" to represent what it does today, and how Euler used it to refer to several different circle constants.